Kunci Jawaban Matematika Kelas 10 Kurikulum Merdeka

Kunci Jawaban – Gunakan Kunci Jawaban Matematika Kelas 10 Kurikulum Merdeka ini untuk menjawab soal Matematika kelas 10 halaman 140, 141 Latihan 5.2 sebagai bahan untuk belajar. Sebelum melihat Kunci Jawaban Matematika Kelas 10 Kurikulum Merdeka halaman 140, 141 ini, ada baiknya siswa mencoba menjawab sendiri terlebih dahulu.

Kunci Jawaban Matematika Kelas 10 Kurikulum Merdeka

KUNCI JAWABAN MATEMATIKA KELAS 10 KURIKULUM MERDEKA

Dikutip dari alumni UIN Maulana Malik Ibrahim Malang (UIN Malang) M Imam Zaenal Abidin, M.Pd berikut adalah kunci jawaban Matematika kelas 10 halaman 140, 141 Latihan 5.2.

1. Bonar memiliki dua pekerjaan paruh waktu. Untuk mengantar barang, Bonar dibayar Rp15.000,00 per jam. Untuk pekerjaan mencuci piring di restoran, Bonar dibayar Rp9.000,00 per jam. Dia tidak dapat bekerja lebih dari 10 jam. Bonar membutuhkan uang sebesar Rp120.000,00.
Berapa jam dia harus bekerja untuk masing-masing pekerjaan?

a. Tuliskan model matematikanya.
Jawaban:
Misalka;
x = lamanya Bonar bekerja mengantar barang dan
y = lamanya Bonar bekerja mencuci piring
maka;
a. Model Matematika:
x + y ≥ 10
15x + 9y ≤ 120
b. Apakah model matematika tersebut merupakan sistem pertidaksamaan linear?
Jawaban:
Sistem pertidaksamaan linear. Semua variabelnya berpangkat 1.
c. Gambarkan grafiknya.
Jawaban:

Grafik Jawaban No. 1c (Buku Kemdikbud)

d. Tentukan koordinat titik-titik potongnya.
Jawaban:
Berpotongan di (5,5)
e. Tentukan daerah yang memenuhi sistem pertidaksamaan linear.
Jawaban:
Daerah yang berwarna ungu pada grafik
f. Apakah Bonar bisa mendapatkan uang yang dia butuhkan dengan bekerja mengantar barang selama 4 jam?
Jawaban:
Tidak. Tidak ada daerah dengan koordinat (4,y) pada daerah hasil (berwarna ungu).
g. Apakah Bonar bisa mendapatkan uang yang dibutuhkan jika bekerja selama 9 jam?
Jawaban:
Ya, titik (9,1) terletak pada daerah hasil (berwarna ungu). Bonar bisa bekerja selama 9 jam sebagai pengantar barang dan 1 jam sebagai pencuci piring untuk mendapatkan uang yang dibutuhkan.

2. Nova membeli pupuk dan tanaman untuk kebunnya. Nova memiliki uang sebesar Rp100.000,00. Setiap kantong pupuk harganya Rp20.000,00 dan setiap tanaman harganya Rp10.000,00. Nova ingin membeli setidaknya 5 tanaman. Berapa banyak tanaman dan pupuk yang dapat Nova beli?

Jawaban:

Jika t adalah banyaknya tanaman yang dibeli dan p adalah banyaknya pupuk yang dibeli, maka sistem pertidaksamaan linearnya adalah
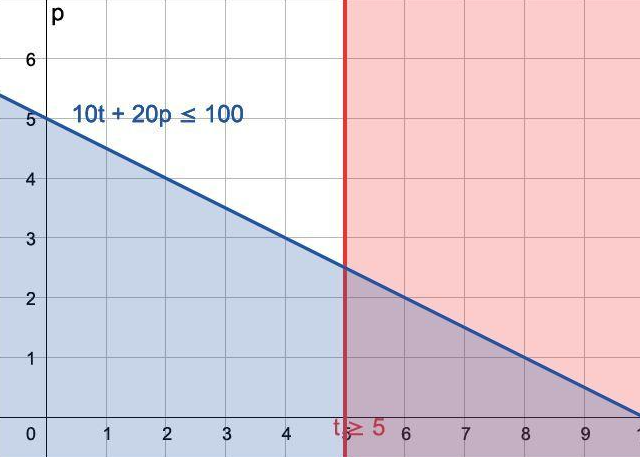
10t + 20p ≤ 100
t ≥ 5
Grafik:

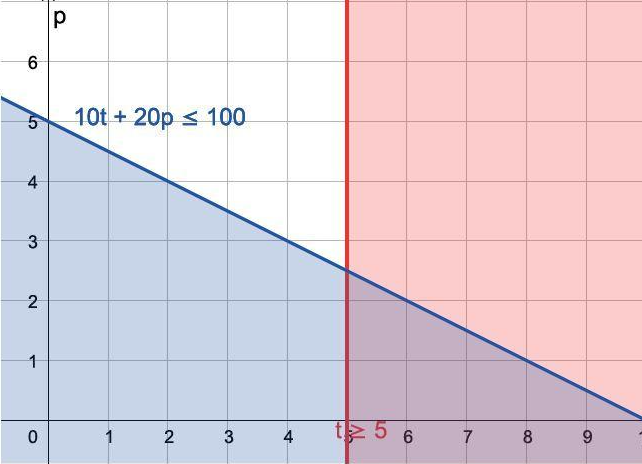
Grafik Jawaban No. 2 (Buku Kemdikbud)

Ada beberapa kemungkinan yang dapat dipilih Nova, contohnya:
– (6,1) artinya 6 kantong pupuk dan 1 tanaman
– (5,2) artinya 5 kantong pupuk dan 2 tanaman

3. Bu Dini membutuhkan telur ayam dan telur puyuh. Telur ayam harganya Rp22.000,00 per kg dan telur puyuh harganya Rp30.000,00 per kg. Bu Dini memiliki uang sebesar Rp150.000,00. Karena khawatir telurnya pecah di perjalanan, Bu Dini tidak mau membawa lebih dari 6 kg telur. Apakah Bu Dini dapat membeli 6 kg telur?

Jawaban:
Jika a adalah berat telur ayam dan p adalah berat telur puyuh yang dibeli, maka
22a + 30p ≤ 150
a + p ≤ 6
Grafik:

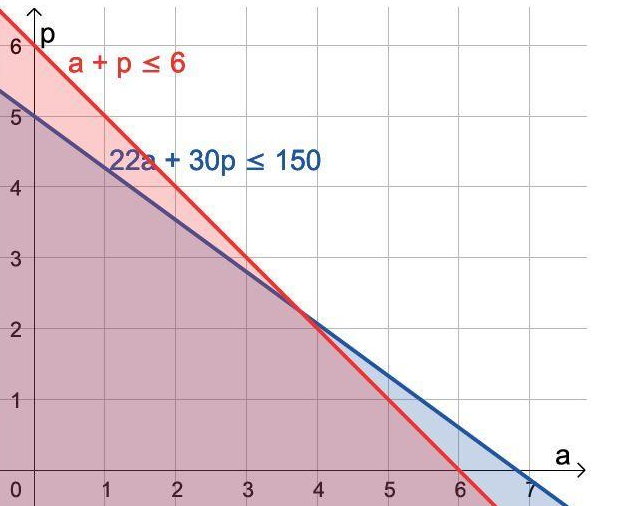
Grafik Jawaban No. 3 (Buku Kemdikbud)

Ada beberapa kemungkinan yang dapat dipilih, contohnya:
– (1,3) artinya 1 kg telur ayam dan 1 kg telur puyuh
– (4,2) artinya 4 kg telur ayam dan 2 kg telur puyuh

4. Sebuah UMKM memproduksi dua jenis sabun cair, yaitu sabun mandi dan sabun cuci tangan. Untuk setiap liter sabun mandi, dibutuhkan biaya produksi Rp15.000,00 per liter. Biaya produksi sabun cuci tangan Rp10.000,00 per liter. Selain itu, pabrik juga harus mengeluarkan biaya tetap sebesar Rp500.000,00.
UMKM tersebut memiliki modal sebesar Rp2.500.000,00. Gudang yang ada dapat menampung 150 liter sabun cair. Sabun mandi dijual seharga Rp25.000,00 per liter dan sabun cuci tangan Rp20.000,00 per liter.
Apakah mereka bisa mendapatkan keuntungan dengan harga tersebut? Berikan contoh banyaknya sabun mandi dan sabun cuci masing-masing yang dijual sehingga pendapatan mereka lebih dari pengeluaran.

Jawaban:
Jika c adalah banyaknya sabun cuci dan m adalah banyaknya sabun mandi. Keuntungan didapatkan jika pendapatan lebih besar dari pengeluaran. Sistem pertidaksamaan linearnya:
10c + 15m + 500 ≤ 2500
c + m ≤ 150
20c + 25m > 10c + 15m + 500
Grafik:

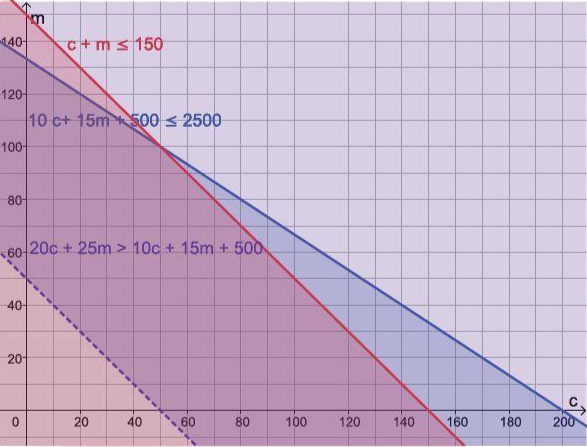
Grafik Jawaban No. 4 (Buku Kemdikbud)

UMKM tersebut bisa mendapat keuntungan, salah satunya jika membuat 80 liter sabun cuci dan 40 liter sabun mandi.

Demikian terkait kunci jawaban Matematika kelas 10 halaman 140, 141 Latihan 5.2 Kurikulum Merdeka full pembahasan 2022. Semoga bermanfaat